N-Body (Undergrad Dissertation project)

Overview

N-Body Simulations aim to study the movement of objects (bodies) under the effect of some governing force, such as gravity. The most common N-Body simulations are of the celestial kind investigating the effects of gravity on celestial bodies. These simulations usually study the linear movement of these bodies and ignore any rotational movement as is not usually important. They also rarely deal with collisions between these bodies. However, Computer games do not ignore these aspects and have to simulate collisions and rotations in real time. Studying optimisations used in N-Body simulations and computer games is it feasible to implement collisions and rotational dynamics into an n-body simulation?

Base Simulation

To answer this question first a base framework had to be made to visualise the N-Body simulation, programming in c++ a basic OpenGl renderer was made.

Collisions

This project implements collisions in two phases to increase efficiency:

• Broad phase: Each body is given a basic bounding volume that allow for quick intersection tests with other bounding volumes. For this project, a bounding sphere was used as it does not require any reorientation of the sphere to match the object’s rotation.
• Narrow phase: If an intersection is detected a more accurate collision check is performed to confirm and resolve the collision. Due to this project using primitive shapes (cuboids) to represent bodies a seperating axis test can be performed to quickly evaluate if two objects aren't colliding, if they are then a novel box to box collision method is used to evalute and resolve the collision.

Due to it being expansive to evaluate and resolve collisions especially with many rigid bodies you ideally want to try and prove a collision is not happening as quickly as possible. This is why a broad and narrow phase is commonly used and implemented within this project.

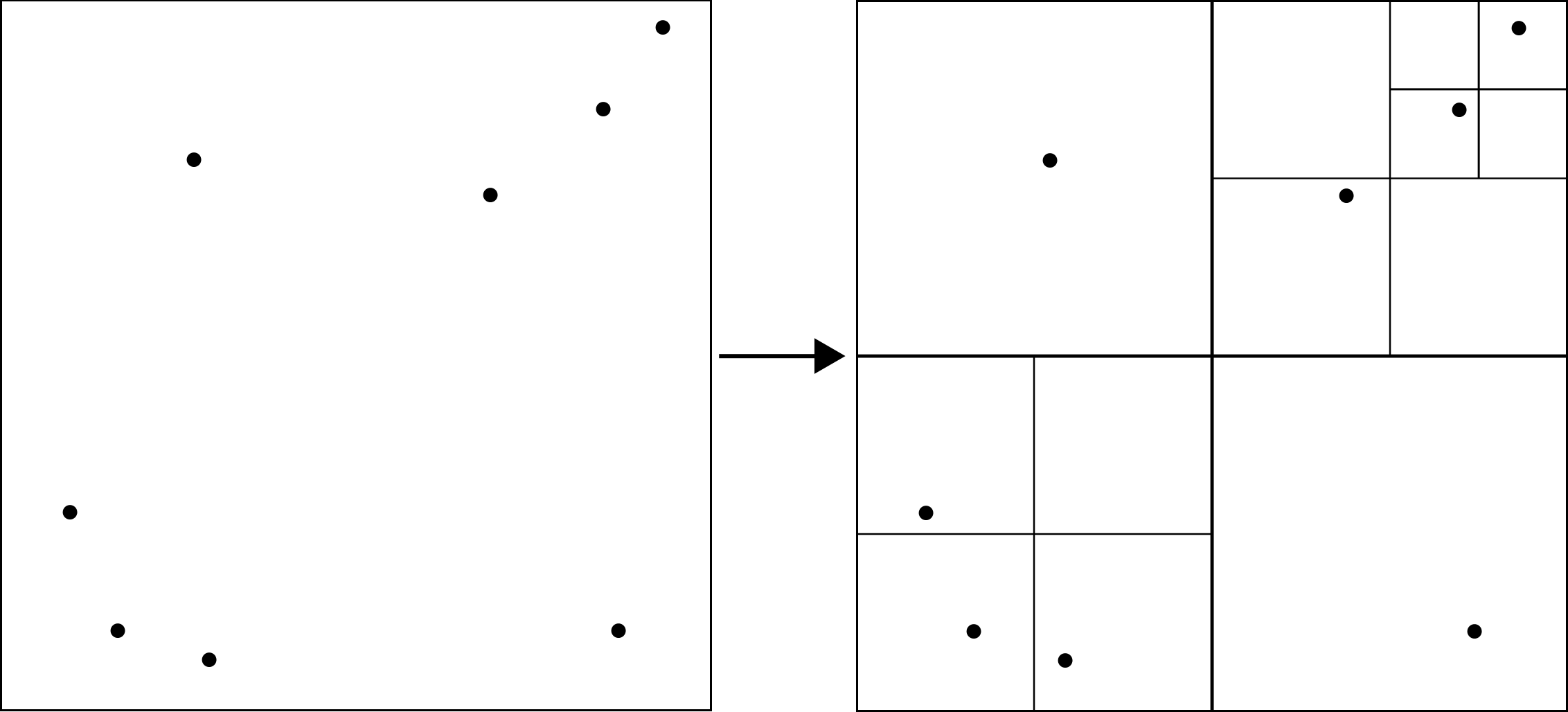
Tree codes

An optimisation common in both collisions and N-body Simulations known as tree codes was implemented to investigate the efficiency gained from such an optimisation. Without the optimisation a brute force approach would need to be taken resulting in a time complexity of O(N²). However, by treating bodies further away from the body being evaluated as a single body, less calculations need to be performed. This is achieved by partitioning the space containing the bodies within a tree data structure to optimise the force calculation. Once partitioned, the force acting upon each body can be calculated and applied more efficiently. This is achieved by calculating the distance between the current body and each node. If the distance is sufficiently large, only one calculation is required to estimate the force experienced by the bodies that lie within that node, instead of calculating the effect of every body. If the node is not sufficiently distant from the current body, then each sub tree is examined recursively until a child node is far enough away, or a child node contains just a single body and that body is evaluated as normal.

As mentioned previously, when dealing with collisions ideally you want to prove a collision is not happening as quickly and as cheaply as possible. Since the space is already being partitioned for the force calculation we can also disregard evaluting collisions between bodies that are within nodes far away from one another.

Futher Improvements

There are several improvements that could potentially increase efficiency of collisions, rotations, and enhance the overall project even further. One of the improvements highlighted would be parallelising the project onto the GPU. Due to the nature of the N-body simulation it lends itself to being parallelised. The force on each body could be calculated almost simultaneously instead of sequentially, depending on the number of threads the GPU has. Collisions could also be parallelised in a similar fashion. Each body could check for a collision, calculate the specifics, and resolve it again almost simultaneously instead of sequentially.